ES Thursday 7-7-16
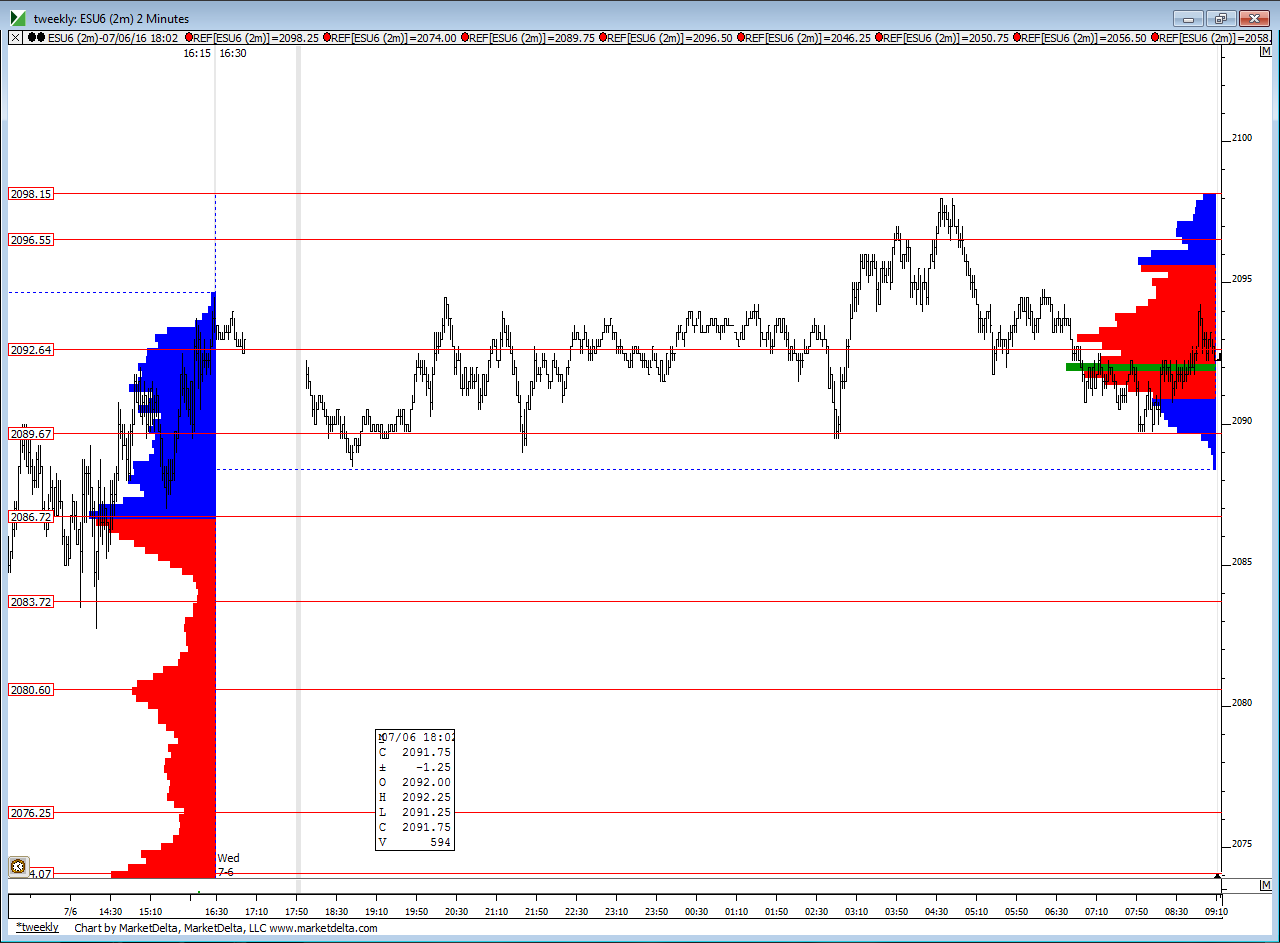
Main bell curve for me has center at 92.50 and an upper edge at 96.50 and a lower edge at 89.50 . so this is not perfectly symetric this morning. The 92.50 is a better magnet price and would prefer to see price push away from that on LOW volume and then have volume dry up to mean revert back to 92.50...86.75 and 83.75 are further numbesr to watch on downside ......ranges are a bit tight and would rather see 4 points between each line but I can only trade what is given. Here is overnight against part of yesterday..I'm using 96.50 - 98.50 as a resistance zone should we get up there as that would include the POC from 7-4 and low time from 7-1 trade...bulls need to hold 86.75 to keep long side in tact today
i still think it going down far than 98.50.i looking for the 1 min bar to be tested as target.
I'm gonna pull it down for ya duck with my massive amounts of selling ...LOL !! but I need to see it get back to the 98 area first ......this is low volume garbage....and so far it's driven away from my 92.50 magnet on Low volume but I haven't been able make great piles of cash today with that idea...I think many are conflicted and the sellers want to keep it under last weeks highs...the last thing we need is to see volume surge on a breakout from that point on the second or third try...
they sucked me in at 2100.25...worst trade location as it is the center of today's developing bell curve....keeping it small as this could tip either way or just drag back and forth to torture us some more
exiting at 98.25 and will try to hold for 96.50 and then last at 92.50...wishful thinking I believe..especially since yd's highs will also be in the way if it does decide to sell off......what am I suppose to have targets at EVERY 2 point increment when I only had 4 contracts on to begin with ? I don't think so !!..no more initiations for me.....good luck from here
thanks bruce for the selling..exit at 95
It was like a fourth of july miracle and they hit the ultimate exit at 11:05...almost on perfect schedule...c ya tomorrow...good trading Duck
bruce it really wasnt good trading on my part..reason is i should of exit at 2100 for the small loss and short again at 2101.25..some days i can take those small losses no problem then other days i like a deer in the head lights. lol i was lucky my 1st stop wasnt hit at 2102.25 too. i am really liking those small losses over the 3-4 point losses..yes i done too today not because of time but of those 6 question you post while ago..i list them again for other people to view
1) over night high or low broken
2)floor trader number hit
3)over night mid point test
4)1st 30 min vpoc
5)s.i.t.y.s
6) break of previous day range
1) over night high or low broken
2)floor trader number hit
3)over night mid point test
4)1st 30 min vpoc
5)s.i.t.y.s
6) break of previous day range
Emini Day Trading /
Daily Notes /
Forecast /
Economic Events /
Search /
Terms and Conditions /
Disclaimer /
Books /
Online Books /
Site Map /
Contact /
Privacy Policy /
Links /
About /
Day Trading Forum /
Investment Calculators /
Pivot Point Calculator /
Market Profile Generator /
Fibonacci Calculator /
Mailing List /
Advertise Here /
Articles /
Financial Terms /
Brokers /
Software /
Holidays /
Stock Split Calendar /
Mortgage Calculator /
Donate
Copyright © 2004-2023, MyPivots. All rights reserved.
Copyright © 2004-2023, MyPivots. All rights reserved.